Part 2 Two-stimulus case with equal variances
2.1 Background information
In this simple scenario, we consider two stimuli that are presented on the skin in two positions and are separated in time. Some basic assumptions of the Bayesian Observer Model are:
- stimuli (on the skin) are never perceived with perfect accuracy because the precision is imperfect and therefore each stimulus perceived with a certain (random) measurement error
- successive stimuli are caused by an object moving along the skin
- objects move at a realistic speed. Or, in other words, it is unlikely that objects move very fast and that stimuli therefore move a far distance in a short time
The second assumption is referred to as the low-velocity prior.
2.1.1 Hypotheses derived from the model
Some hypotheses that can be derived from the described model are:
- stimuli that are presented far apart and fast will be perceptually attracted towards each other, i.e. there is a perceptual length contraction
- the faster the stimulation, the stronger is the length contraction
- the further the traveled distance, the stronger the length contraction
- the higher the precision, the weaker the length contraction
- the stronger the low-velocity prior, the stronger the length contraction
2.2 Parameters
The model includes the following parameters:
- \(x_{1m}\) and \(x_{2m}\) as the “measured” positions, i.e. the estimate given by the sensors corresponding to the stimulus positions
- \(x_1\) and \(x_1\) as the inferred or hypothetical stimulus positions
- \(t\) as the time (in seconds) passing between the taps
- \(\sigma_s\) the spatial standard deviation, or uncertainty, referring to the sensed positions (\(x_{1m}\) and \(x_{2m}\)). Higher values indicate lower precision.
- \(\sigma_v\) the degree of the “low-velocity.” Lower values indicate slower expected speed.
A word about units: Although the units of time and space are arbitrary as long as they are consistent, there is a consistent use of units in the literature. Usually, all spatial units \(x_{1m}\), \(x_{2m}\), \(x_1\), \(x_1\), and \(\sigma_s\) are expressed in cm units. And time, \(t\) is expressed as seconds. The low-velocity prior \(\sigma_v\) is expressed as space per time units and when using cm and seconds would be cm/s. The \(\sigma_s\) is sometimes conceptually referred to as the average localization error, e.g. with reference to The paper by Weinstein (1968) with 1 cm. Strictly speaking, however, it refers to the standard deviation, or variable error, of spatial localization.
2.3 Formula for prior distribution
In the appendix, the formula for the prior distribution is given in Formula A08 as:
\[p(x_1,x_2|t) \propto p(x_2|x_1,t) = \frac {1} {\sqrt{2\pi}\sigma_vt} exp(-\frac {(x_2-x_1)^2}{2(\sigma_v t)^2})\]
2.4 Formula for the likelihood distribution
The formula for the likelihood distribution is given in Formula A10 as: \[p(x_{1m},x_{2m}|x_1, x_2, t) = p(x_2|x_1,t) = p(x_{1m}|x_1)*p(x_{2m}|x_2)\] And these two conditional probabilities are defined in A11 as: \[p(x_{1m}|x_1) = \frac {1} {\sqrt{2\pi}\sigma_s} exp \left(-\frac {(x_{1m}-x_1)^2}{2\sigma_s^2} \right)\] and \[p(x_{2m}|x_2) = \frac {1} {\sqrt{2\pi}\sigma_s} exp \left(-\frac {(x_{2m}-x_2)^2}{2\sigma_s^2}\right)\]
Following logically from this, the likelihood computes as: \[p(x_{1m},x_{2m}|x_1, x_2, t) = \frac {1} {\sqrt{2\pi}\sigma_s} exp \left(-\frac {(x_{2m}-x_2)^2}{2\sigma_s^2}\right) * \frac {1} {\sqrt{2\pi}\sigma_s} exp \left(-\frac {(x_{2m}-x_2)^2}{2\sigma_s^2} \right)\]
2.5 Formula for the posterior distribution
The formula for the posterior distribution is given in A13 as: \[p(x_1, x_2|x_{1m},x_{2m}, t) \propto exp \left( - \left( \frac {(x_{1m} - x_1)^2 + (x_{2m} - x_2)^2} {2\sigma_s ^2} + \frac {(x_2-x_1)^2}{(2\sigma_v t)^2} \right) \right)\]
The formula for the posterior distribution is also formulated in in A14 as:
\[p(x_1, x_2|x_{1m},x_{2m}, t) \propto exp \left( -\frac {1} {2(1-\rho ^2)} \left( \frac {(x_1 - x_{1*})^2 + (x_2 - x_{2*})^2 - 2 \rho (x_1 - x_{1*}) (x_2 - x_{2*})} {\sigma ^2} \right) \right)\] However, some unknowns appear in this equation which are defined further down in A14. The posterior modes, denoted as \(x_{1*}\) and \(x_{2*}\) are defined as:
\[x_{1*}=x_{1m} \left( \frac {(\sigma_v t)^2 + \sigma_s ^2} {(\sigma_v t)^2 + 2\sigma_s ^2} \right) + x_{2m} \left( \frac {\sigma_s^2} {(\sigma_v t)^2 + 2\sigma_s ^2} \right)\] and: \[x_{2*}=x_{2m} \left( \frac {(\sigma_v t)^2 + \sigma_s ^2} {(\sigma_v t)^2 + 2\sigma_s ^2} \right) + x_{1m} \left( \frac {\sigma_s^2} {(\sigma_v t)^2 + 2\sigma_s ^2} \right)\]
The correlation between the Gaussian distributions \(\rho\) is given as:
\[\rho = \frac {\sigma_s^2} {\sigma_s^2 + (\sigma_v t)^2} \] Finally, the combined variance \(\sigma^2\) is given as:
\[\sigma^2 = \sigma_s^2 \frac {\sigma_s^2 + (\sigma_v t)^2} {2\sigma_s^2 + (\sigma_v t)^2}\]
2.6 R implementations of the formulae
The following code implements formula A08, A11 and A13, respectively. The posterior and posterior modes can alternatively also be computed via formula A14.
Note: the R functions preented below can also compute several values at a time, if the parameters are passed as vectors. You will see applications of that in the exaamples below.
2.6.1 Prior distribution
#formula A08
computePrior <- function(x1, x2, sigma_v, time_t) {
Prior <- 1/(sqrt(2*pi)*sigma_v*time_t) * exp(-(x2-x1)^2/(2*(sigma_v*time_t)^2))
return(Prior)
}2.6.2 Likelihood distribution
#formula A11
computeLikelihood <- function(x1m, x2m, x1, x2, sigma_s) {
p_x1m_given_x1 <- 1/(sqrt(2*pi)*sigma_s) * exp(-(x1m-x1)^2/(2*sigma_s^2))
p_x2m_given_x2 <- 1/(sqrt(2*pi)*sigma_s) * exp(-(x2m-x2)^2/(2*sigma_s^2))
Likelihood <- p_x1m_given_x1*p_x2m_given_x2
return(Likelihood)
}2.6.3 Posterior distribution
#formula A13
computePosterior <- function(x1m, x2m, x1, x2, sigma_s, sigma_v, time_t) {
Posterior <- exp(-(((x1m-x1)^2+(x2m-x2)^2)/(2*sigma_s^2) + (x2-x1)^2/(2*(sigma_v*time_t)^2)))
return(Posterior)
}#formula A14
compute_x1_star <- function(x1m, x2m, sigma_s, sigma_v, time_t) {
x1_star <- x1m * (((sigma_v*time_t)^2+sigma_s^2) / ((sigma_v*time_t)^2+2*sigma_s^2)) + x2m * (sigma_s^2 / ((sigma_v*time_t)^2+2*sigma_s^2))
return(x1_star)
}
compute_x2_star <- function(x1m, x2m, sigma_s, sigma_v, time_t) {
x2_star <- x1m * (sigma_s^2 / ((sigma_v*time_t)^2+2*sigma_s^2)) + x2m * (((sigma_v*time_t)^2+sigma_s^2) / ((sigma_v*time_t)^2+2*sigma_s^2))
return(x2_star)
}
compute_common_sigma_square <- function(sigma_s, sigma_v, time_t) {
sigma_square <- sigma_s^2 * (sigma_s^2 + (sigma_v*time_t)^2) / (2*sigma_s^2 + (sigma_v*time_t)^2)
return(sigma_square)
}
compute_correlation <- function(sigma_s, sigma_v, time_t) {
distr_correlation <- sigma_s^2 / (sigma_s^2 + (sigma_v*time_t)^2)
return(distr_correlation)
}
computePosterior2 <- function(x1m, x2m, x1, x2, sigma_s, sigma_v, time_t, returnList=F) {
#first compute the necessary variables
x1_star <- compute_x1_star(x1m = x1m, x2m = x2m, sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
x2_star <- compute_x2_star(x1m = x1m, x2m = x2m, sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
common_sigma_square <- compute_common_sigma_square(sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
correlation <- compute_correlation (sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
#now use formula 14 to compute posterior
Posterior <- exp( ( - 1/(2*(1-correlation^2)) *
( ((x1-x1_star)^2) + (x2-x2_star)^2 - 2*correlation *
(x1-x1_star)*(x2-x2_star) )/common_sigma_square ) )
if (returnList==T) {
#extend to be a list
returnList <- list( x1_star= x1_star, x2_star=x2_star,
common_sigma_square=common_sigma_square, correlation=correlation,
Posterior = Posterior )
return(returnList)
} else {
return(Posterior)
}
}2.7 Test of formulae
The following code will test the formulae to evaluate whether the output makes sense.
2.7.1 Used model parameters
x1 <- 3
x2 <- 7
x1m <- 3
x2m <- 7
sigma_s <- 1 #spatial resolution as used for Figure 2
sigma_v <- 10 #low speed prior
time_t <- 0.15 #seconds passing between taps2.7.2 Compute Prior, Likelihood and Posterior
#single point values
computePrior(x1 = x1, x2 = x2, sigma_v = sigma_v, time_t = time_t) ## [1] 0.007597324computeLikelihood(x1 = x1, x2 = x2, x1m = x1, x2m = x2, sigma_s = sigma_s)## [1] 0.1591549computePosterior(x1m = x1, x2m = x2, x1 = x1, x2 = x2, sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)## [1] 0.0285655#and the alternative version
computePosterior2(x1m = x1, x2m = x2, x1 = x1, x2 = x2,
sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t, returnList=T)## $x1_star
## [1] 3.941176
##
## $x2_star
## [1] 6.058824
##
## $common_sigma_square
## [1] 0.7647059
##
## $correlation
## [1] 0.3076923
##
## $Posterior
## [1] 0.1876451Note that the absolute values derived from the functions “computePosterior” (based on formula A13) and “computePosterior2” (based on A14) are not identical. In the end, however, it does not matter because the probabilities themselves are not valid anyway because it the given sign is “proportional to” \(\propto\). Note in the plot in the next section that the distributions themselves would be identical when they are normalized (transformed so that the sum of all values equals 1).
2.8 Reproduce Figure 2
In the following, we reproduce Figure 2 from (Goldreich and Tong 2013). The following parameters are used in the article and are used here for plotting.
#params for plots
x1_range <- c(0, 10)
x2_range <- c(0, 10)
#resolution for graphs
x1_res <- 100
x2_res <- 100Compute the values fot the whole matrix
#prior
priorMat <- expand.grid(x1=seq(x1_range[1], x1_range[2], length.out = x1_res),
x2=seq(x2_range[1], x2_range[2], length.out = x2_res))
priorMat$p <- computePrior(x1 = priorMat$x1, x2 = priorMat$x2, sigma_v = sigma_v, time_t = time_t)
#likelihood
likelihoodMat <- expand.grid(x1=seq(x1_range[1], x1_range[2], length.out = x1_res),
x2=seq(x2_range[1], x2_range[2], length.out = x2_res))
likelihoodMat$p <- computeLikelihood(x1m = x1m, x2m = x2m,
x1 = likelihoodMat$x1, x2 = likelihoodMat$x2, sigma_s = sigma_s)
#posterior
posteriorMat <- expand.grid(x1=seq(x1_range[1], x1_range[2], length.out = x1_res),
x2=seq(x2_range[1], x2_range[2], length.out = x2_res))
posteriorMat$p <- computePosterior(x1m = x1m, x2m = x2m,
x1 = posteriorMat$x1, x2 = posteriorMat$x2,
sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
posteriorMat$p2 <- computePosterior2(x1m = x1m, x2m = x2m,
x1 = posteriorMat$x1, x2 = posteriorMat$x2,
sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)Now create a plot of all three distributions (like in Figure 2). We add a fourth one to demonstrate that both formulae for the posterior distribution lead to similar distributions.
#prior
prior.plot <- ggplot(priorMat, aes(x=x1, y=x2, fill=p)) +
geom_raster() +
coord_fixed() +
ggtitle("prior")
#likelihood
likelihood.plot <- ggplot(likelihoodMat, aes(x=x1, y=x2, fill=p)) +
geom_raster() +
coord_fixed() +
ggtitle("likelihood") +
geom_point(x=x1, y=x2, size=2, color="white", shape=21, fill=NA) #real position
#posterior
Posterior_mode_x1 <- compute_x1_star(x1m = x1m, x2m = x2m,
sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
Posterior_mode_x2 <- compute_x2_star(x1m = x1m, x2m = x2m,
sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
#version based on A13
posterior.plot <- ggplot(posteriorMat, aes(x=x1, y=x2, fill=p)) +
geom_raster() +
coord_fixed() +
ggtitle("posterior") +
geom_point(x=x1, y=x2, size=2, color="white", shape=21, fill=NA) + #real position
geom_point(x=Posterior_mode_x1 , y=Posterior_mode_x2, size=2, color="red", shape=21, fill=NA) #posterior mode
#version based on A14
posterior.plot2 <- ggplot(posteriorMat, aes(x=x1, y=x2, fill=p2)) +
geom_raster() +
coord_fixed() +
ggtitle("posterior2") +
geom_point(x=x1, y=x2, size=2, color="white", shape=21, fill=NA) + #real position
geom_point(x=Posterior_mode_x1 , y=Posterior_mode_x2, size=2, color="red", shape=21, fill=NA) #posterior mode
#create a panel
cowplot::plot_grid(prior.plot, likelihood.plot, posterior.plot, posterior.plot2)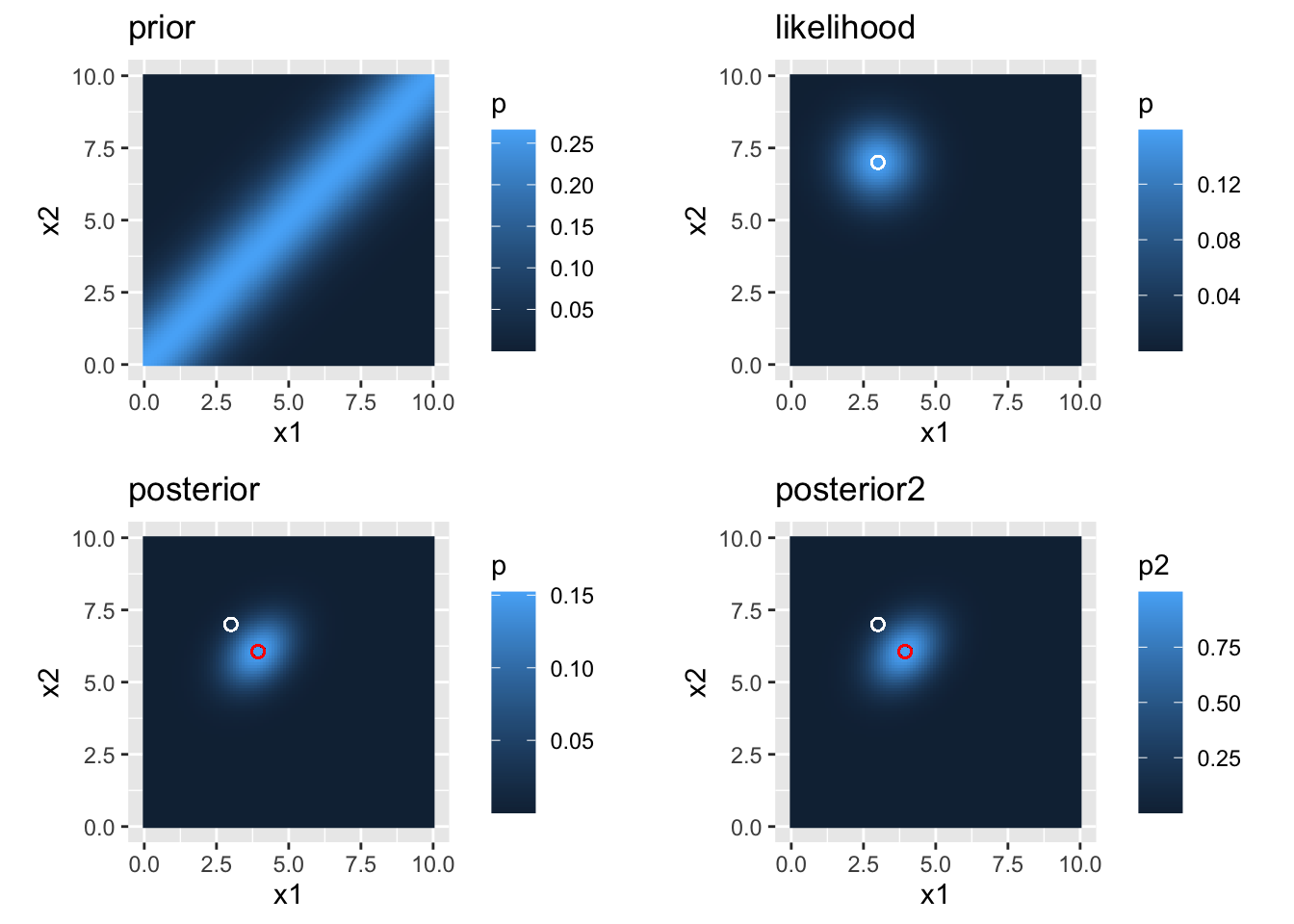
Figure 2.1: prior, likelihood, and posterior distributions
The figure looks just like in the article.
2.8.1 Numerical sanity check
As a quick sanity check: compare the analytically dtermined posterior mode to the one that can be seen in the figure. This can simply be done by finding the value with the highest posterior probability numerically and chhecking where it is.
#Posterior mode determined analytically
Posterior_mode_x1 <- compute_x1_star(x1m = x1m, x2m = x2m,
sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
Posterior_mode_x2 <- compute_x2_star(x1m = x1m, x2m = x2m,
sigma_s = sigma_s, sigma_v = sigma_v, time_t = time_t)
print(paste("analytical values for x1:",
round(Posterior_mode_x1, 3),
"\n and for x2:",
round(Posterior_mode_x2, 3)))## [1] "analytical values for x1: 3.941 \n and for x2: 6.059"#Posterior mode determined numerically
posteriorMax <- max(posteriorMat$p)
posteriorMax.index <- which(posteriorMat$p==posteriorMax)
print(paste("numerical values for x1:",
round(posteriorMat$x1[posteriorMax.index], 3),
"\n and for x2:",
round(posteriorMat$x2[posteriorMax.index], 3)))## [1] "numerical values for x1: 3.939 \n and for x2: 6.061"We can see that the values match quite well.
2.9 Addressing the hypotheses
In this section we will evaluate the hypotheses mentioned above by varying model parameters.
2.9.1 Stimuli that are presented far apart and fast will be perceptually attracted towards each other
This hypothesis is inherently confirmed in the computations above: note that the veridical stimuli were presented at positions of 3 and 7 cm, respectively. This is a distance of 4 cm. The posterior modes were at about 3.9 and 6.1 cm. This is only a distance of 2.2 cm. The model accordingly predicts a length contraction of 4 - 2.2 = 1.8 cm for this set of parameters.
2.9.2 The faster the stimulation, the stronger is the length contraction
To address this point, we repeat the model estimations for different values of \(t\), the time passing between the two taps.
modelData <- data.frame(x1m=3, x2m=7, sigma_s=1, sigma_v=10, time_t=seq(0, 2, length.out=21))
#compute posterior modes
modelData$pm_x1 <- with(modelData, compute_x1_star(x1m, x2m, sigma_s, sigma_v, time_t))
modelData$pm_x2 <- with(modelData, compute_x2_star(x1m, x2m, sigma_s, sigma_v, time_t))
modelData %>%
pivot_longer(cols = c(pm_x1, pm_x2), names_to = "posterior", values_to = "position") %>%
ggplot(aes(x=time_t, y=position, color=posterior)) +
geom_hline(yintercept = 7, linetype=2, color="grey") +
geom_hline(yintercept = 3, linetype=2, color="grey") +
geom_point() +
geom_path() 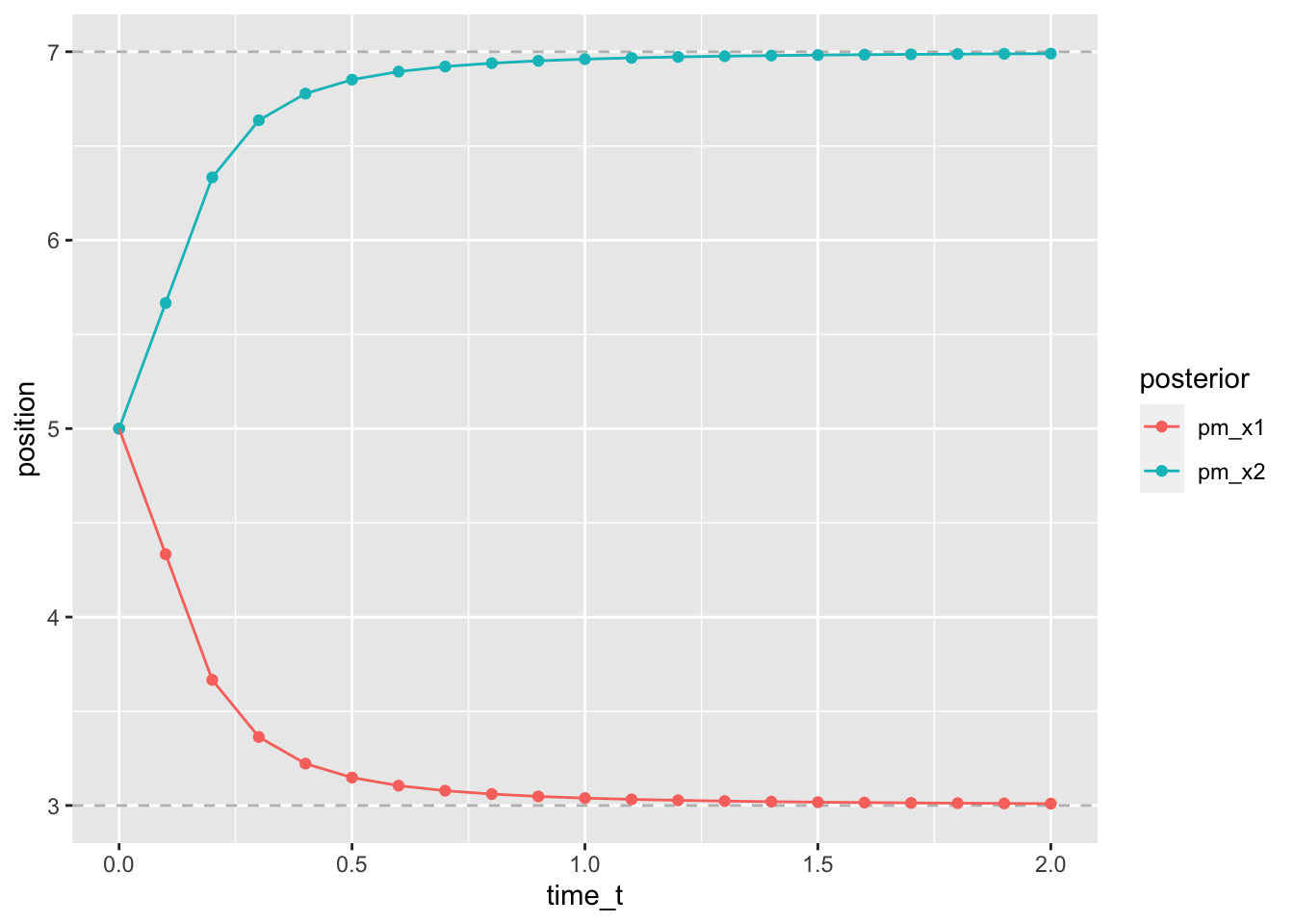
Figure 2.2: stronger contraction at shorter time t
As can be seen from the figure, the attraction of the stimuli towards each other and the according length contraction is strong for short time intervals between the stimuli and disappears for delays of one second or more.
2.9.3 The further the travelled distance, the stronger the length contraction
To show predictions for this scenario, we keep t and sigma_s constant and vary the positions of the taps. Note that due to the small scale, we have decreased the sigma_s parameter to 0.1 to emphasize the effect.
modelData <- data.frame(x1m=0, x2m=seq(0.1, 1, length.out=10), sigma_s=0.1, sigma_v=10, time_t=0.015)
#compute posterior modes
modelData$pm_x1 <- with(modelData, compute_x1_star(x1m, x2m, sigma_s, sigma_v, time_t))
modelData$pm_x2 <- with(modelData, compute_x2_star(x1m, x2m, sigma_s, sigma_v, time_t))
p1 <- modelData %>%
pivot_longer(cols = c(pm_x1, pm_x2), names_to = "posterior", values_to = "position") %>%
ggplot(aes(x=x2m, y=position, color=posterior)) +
geom_abline(intercept = 0, slope = 1, linetype=2, color="grey") +
coord_fixed() +
xlim(0, 1) + ylim(0, 1) +
geom_point() +
geom_path() +
ggtitle("posterior modes for \nvarying veridical distances")
#and another plot of the real distance vs. perceived distance
##compute real and perceived distances
modelData <- modelData %>% mutate(veridical=x2m-x1m, perceived=pm_x2-pm_x1)
p2 <- modelData %>%
ggplot(aes(x=veridical, y=perceived)) +
coord_fixed() +
xlim(0, 1) + ylim(0, 1) +
geom_point() +
geom_path() +
ggtitle("veridical vs. perceived \ndistances")
#merge plots
plot_grid(p1, p2, nrow = 1, labels = c("a", "b"), rel_widths = c(1, 0.75))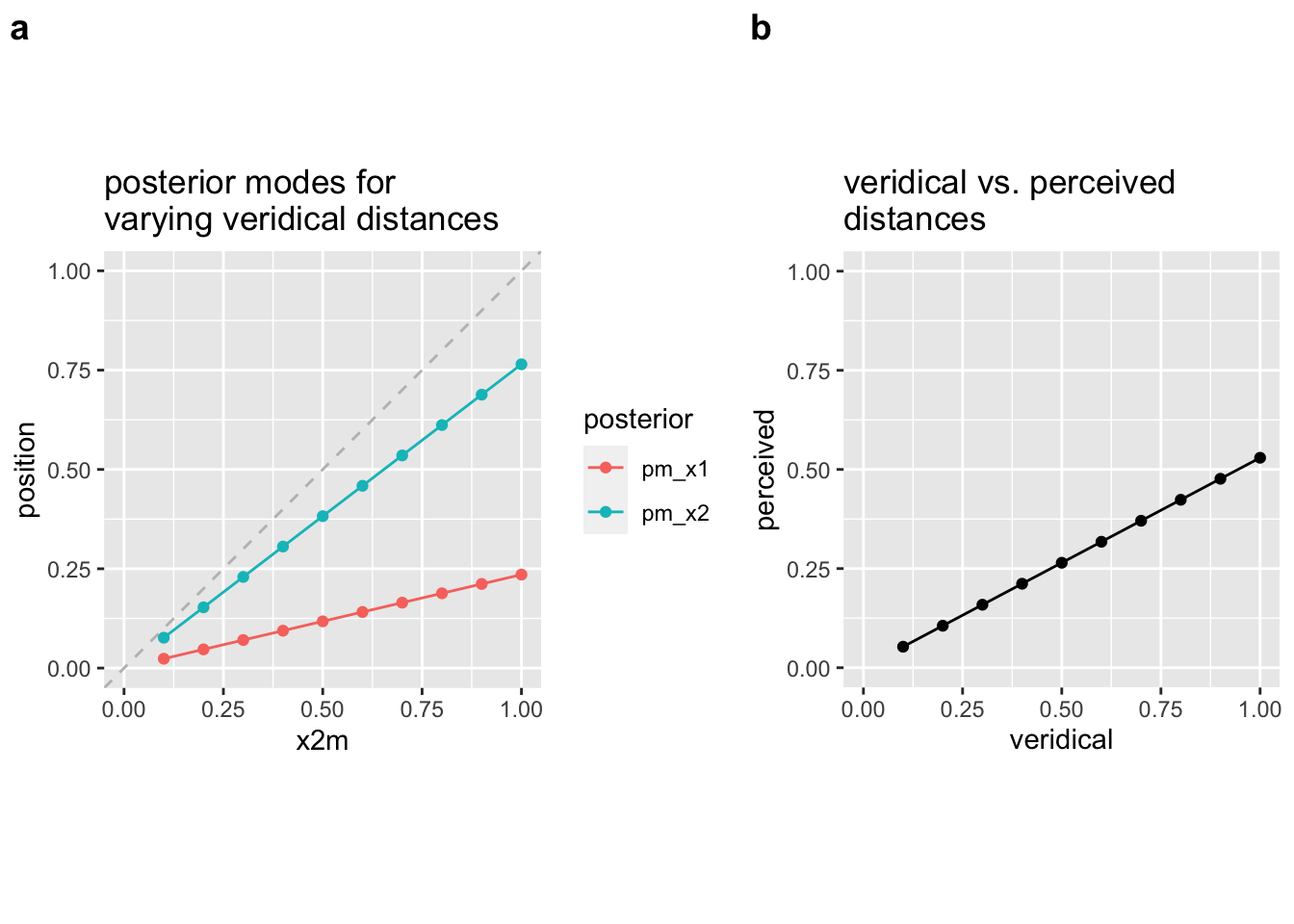
Figure 2.3: stronger (relative) contraction for larger distances
2.9.4 The higher the precision, the weaker the length contraction
This time we keep parameters all parameters constant except for the sigma_s.
modelData <- data.frame(x1m=3, x2m=7, sigma_s=seq(0, 2, length.out=21), sigma_v=10, time_t=0.15)
#compute posterior modes
modelData$pm_x1 <- with(modelData, compute_x1_star(x1m, x2m, sigma_s, sigma_v, time_t))
modelData$pm_x2 <- with(modelData, compute_x2_star(x1m, x2m, sigma_s, sigma_v, time_t))
modelData %>%
pivot_longer(cols = c(pm_x1, pm_x2), names_to = "posterior", values_to = "position") %>%
ggplot(aes(x=sigma_s, y=position, color=posterior)) +
geom_hline(yintercept = 7, linetype=2, color="grey") +
geom_hline(yintercept = 3, linetype=2, color="grey") +
geom_point() +
geom_path() 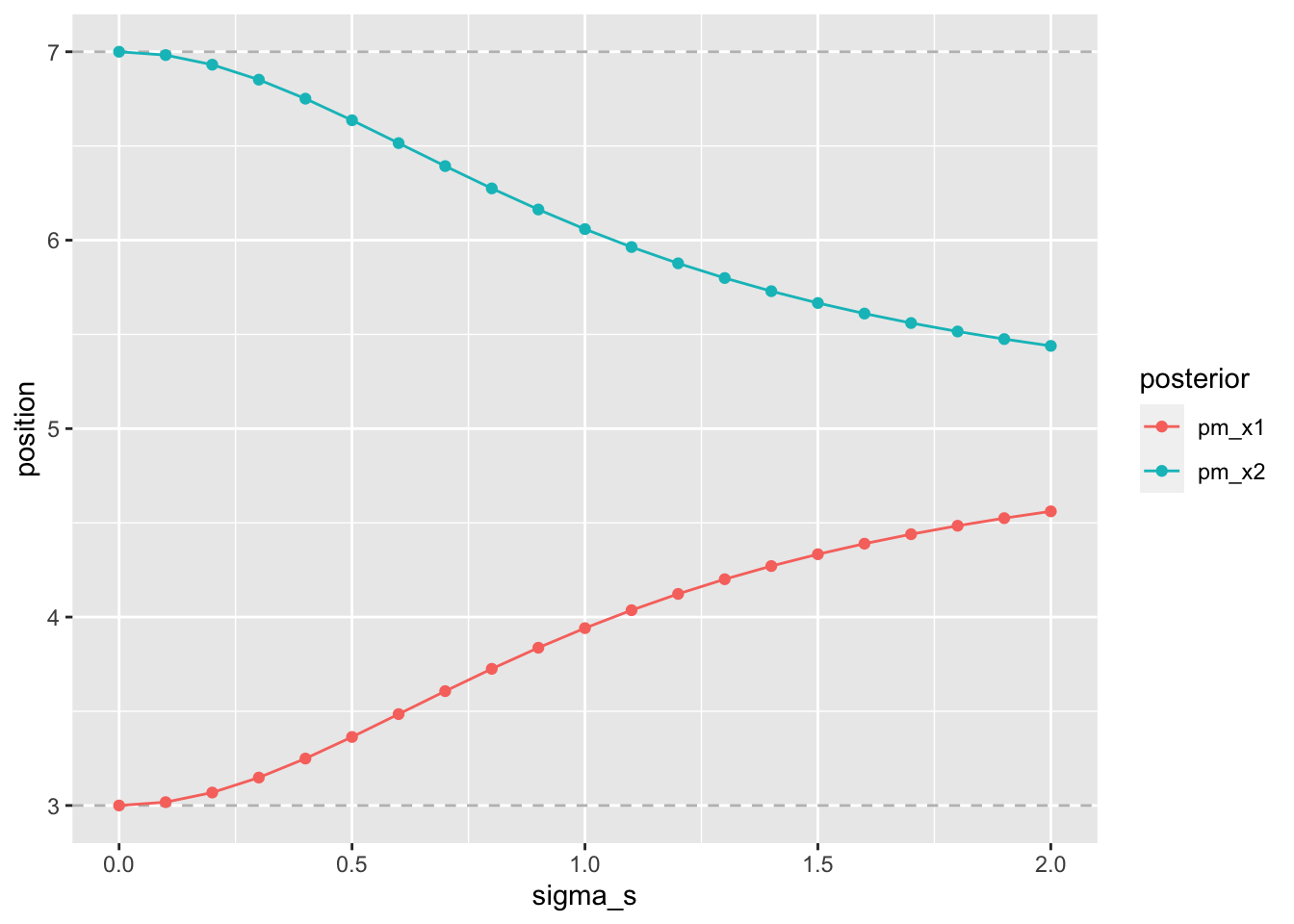
Figure 2.4: stronger contraction for lower precision
2.9.5 The stronger the low-velocity prior, the stronger the length contraction
Finally, the low-velocity prior is varied as the only parameter.
modelData <- data.frame(x1m=3, x2m=7, sigma_s=1, sigma_v=seq(0, 10, length.out=21), time_t=0.15)
#compute posterior modes
modelData$pm_x1 <- with(modelData, compute_x1_star(x1m, x2m, sigma_s, sigma_v, time_t))
modelData$pm_x2 <- with(modelData, compute_x2_star(x1m, x2m, sigma_s, sigma_v, time_t))
modelData %>%
pivot_longer(cols = c(pm_x1, pm_x2), names_to = "posterior", values_to = "position") %>%
ggplot(aes(x=sigma_v, y=position, color=posterior)) +
geom_hline(yintercept = 7, linetype=2, color="grey") +
geom_hline(yintercept = 3, linetype=2, color="grey") +
geom_point() +
geom_path() 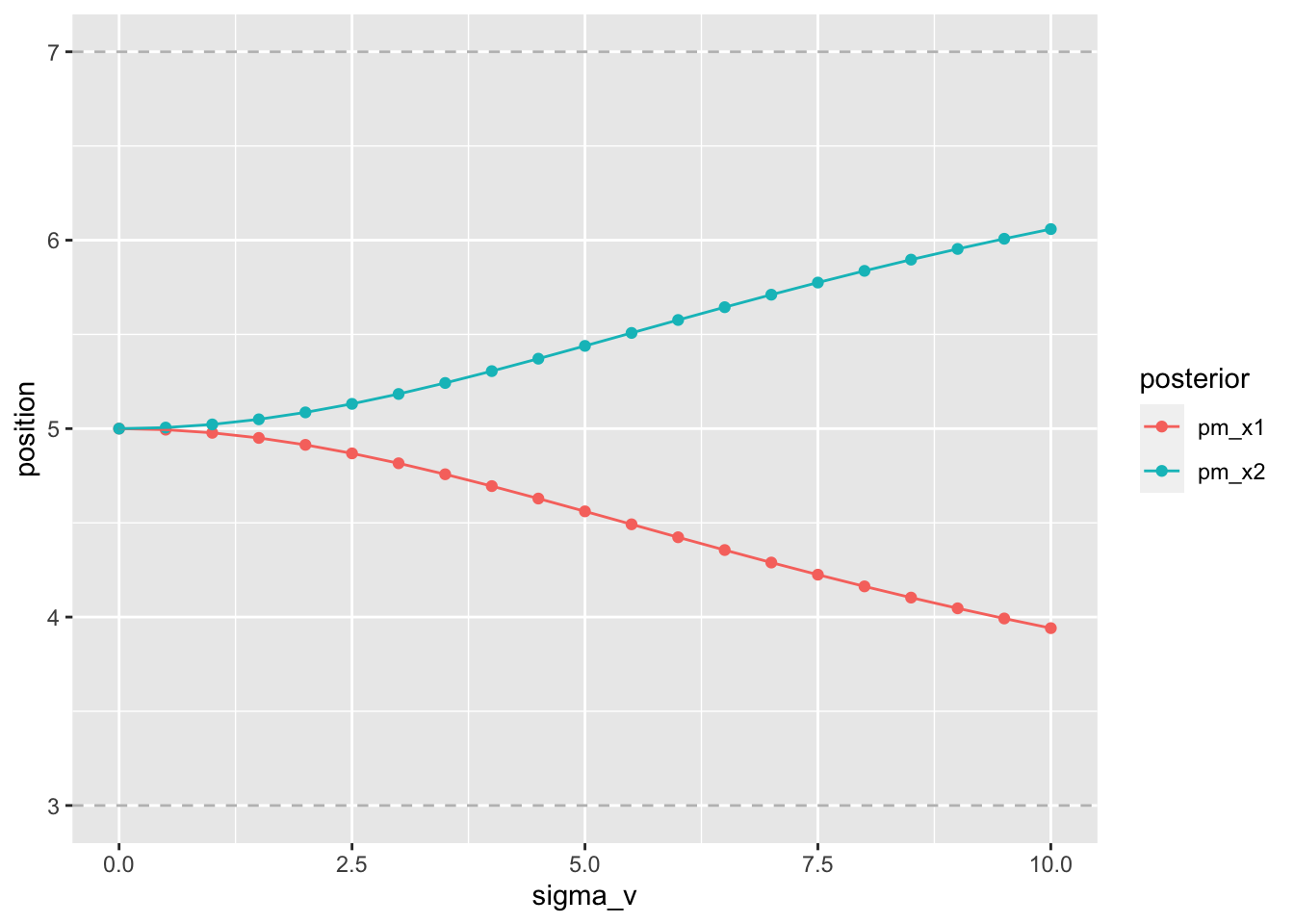
Figure 2.5: stronger contraction for lower expected velocity